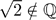Von der Irrationalität von

Ein p aus N sei existent und q aus Z, das nicht verschwinde, sodass sich p als Dividend mit q zu einem Bruch verbinde.
Nicht genug der Forderungen, eines vorher noch erwäge: Dann erst sei der Bruch gelungen, wenn im Quadrat sich 2 ergäbe.
Doch dieses führt zum Widerspruch. "Warum nur?", fragst du - ganz zurecht. Dazu betrachte unser'n Bruch - unmöglich wird er dem gerecht.
Es bleibt, das ist schnell nachgedacht, die Allgemeinheit unbeschränkt, wenn der Bruch grad so gemacht, dass als gekürzt man ihn erkennt.
Der Bruch, quadriert, muss 2 erreichen. Das Doppelte von q hoch 2 der zweiten p-Potenz muss gleichen. Beides, klar, ist einerlei.
Daraus folgt, dass p gerade. Als 2 mal k man denk' es sich. Kürzt man die Gleichung, sieht man - schade! - der Widerspruch zeigt sein Gesicht.
Denn 2 teilt niemals q und p, da haben wir es - q.e.d.!
Lutz Büch